2024-5-23 00:0:3 Author: hackernoon.com(查看原文) 阅读量:1 收藏
Authors:
(1) Hans van Haren, NIOZ Royal Netherlands Institute for Sea Research, P.O. Box 59, 1790 AB Den Burg, the Netherlands.
Table of Links
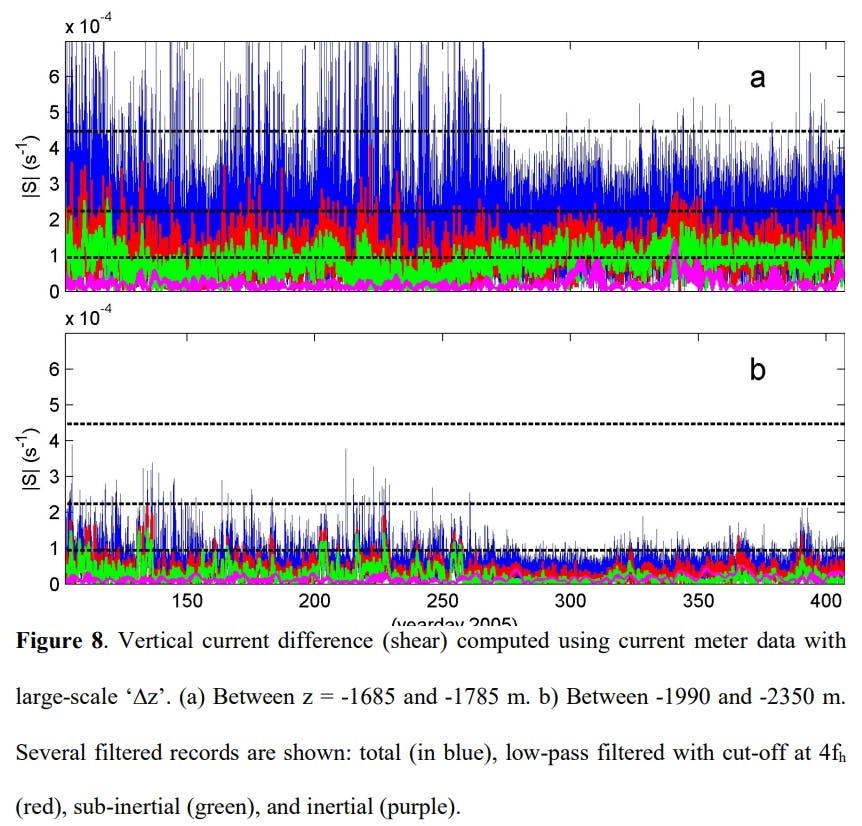
6 Conclusions



Acknowledgments I thank the crews of the R/V Thethys II and Le Suroît for the sea operations, G. Rougier and C. Millot for preparing the ‘GYROSCOP-2’ mooring, and T. Gerkema for providing the model results. I gratefully acknowledge support from the Netherlands organisation for the advancement of scientific research, NWO, and Centre National de la Recherche Scientifique, CNRS, under the (alas no longer existing) French Dutch scientific collaboration.
References
Abarbanel HDI, Holm DD, Marsden JE, Ratiu T (1984) Richardson number criterion for the nonlinear stability of three-dimensional stratified flow. Phys Rev Lett 52:2352-2355
Dengler M, Quadfasel D (2002) Equatorial deep jets and abyssal mixing in the Indian Ocean. J Phys Oceanogr 32:1165-1180
Gascard J-C (1973) Vertical motions in a region of deep water formation. Deep-Sea Res 20:1011-1027
Gerkema T, Shrira VI (2005) Near-inertial waves on the “nontraditional” plane. J Geophys Res 110:C01003. doi:10.1029/2004JC002519
Gerkema T, Exarchou E (2008) Internal-wave properties in weakly stratified layers. J Mar Res 66:617-644
Gerkema T, Zimmerman JTF, Maas LRM, van Haren H (2008) Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev Geophys 46:RG2004. doi:10.1029/2006RG000220
Gill AE (1982) Atmosphere-Ocean Dynamics. Academic Press, San Diego, pp 1-680
Gonella J (1972) A rotary-component method for analysing meteorological and oceanographic vector time series. Deep-Sea Res 19:833-846
Howard LN (1961) Note on a paper of John W. Miles. J. Fluid Mech 10:509-512
LeBlond PH, Mysak LA (1978) Waves in the ocean. Elsevier, Amsterdam, pp 1-602
Marshall J, Schott F (1999) Open-ocean convection: observations, theory, and models. Rev Geophys 37:1-64
Matsuno T, Endoh T, Hibiya T, Sengyu T, Watanabe M (2015) Formation of the well‑mixed homogeneous layer in the bottom water of the Japan Sea. J Oceanogr 71:441-447
Miles JW (1961) On the stability of heterogeneous shear flows. J Fluid Mech 10:496-508
Millot C (1999) Circulation in the Western Mediterranean Sea. J Mar Sys 20:423-442
Millot C, Monaco A (1984) Deep strong currents and sediment transport in the Northwestern Mediterranean Sea. Geo-Mar Lett 4:13-17
Morozov EG, Velarde MG (2008) Inertial oscillations as deep ocean response to hurricanes. J Oceanogr 64:495-509
Munk WH (1980) Internal wave spectra at the buoyant and inertial frequencies. J Phys Oceanogr 10:1718-1728
Saint-Guily B (1970) On internal waves, effects of the horizontal component of the Earth’s rotation and of a uniform current. D Hyd Z 23:16-23
Schott F, Leaman K (1991) Observations with moored acoustic Doppler current profilers in the convection regime in the Golfe du Lion. J Phys Oceanogr 21:558-574
Shay LK, Elsberry RL (1987) Near-inertial ocean current response to hurricane Frederic. J Phys Oceanogr 17:1249-1269
Sheremet VA (2004) Laboratory experiments with tilted convective plumes on a centrifuge: a finite angle between the buoyancy and the axis of rotation. J Fluid Mech 506:217-244
Straneo F, Kawase M, Riser SC (2002) Idealized models of slantwise convection in a baroclinic flow. J Phys Oceanogr 32:558-572
Talley LD, Lohmov V, Ponomarev V, Salyuk A, Tishchenko P, Zhabin I, Riser S (2009) Deep convection and brine rejection in the Japan Sea. Geophys Res Lett 30:1159. doi: 10.1029/2002GL016451
Timmermans M-L, Melling H, Rainville L (2007) Dynamics in the deep Canada Basin, Arctic Ocean, inferred by thermistor chain time series. J Phys Oceanogr 37:1066-1076
van Haren H (2006) Asymmetric vertical internal wave propagation. Geophys Res Lett 33:L06618. doi:10.1029/2005GL025499
van Haren H (2008) Abrupt transitions between gyroscopic and internal gravity waves: the mid-latitude case. J Fluid Mech 598:67-80
van Haren H, Millot C (2004) Rectilinear and circular inertial motions in the Western Mediterranean Sea. Deep-Sea Res I 51:1441-1455
van Haren H, Millot C (2005) Gyroscopic waves in the Mediterranean Sea. Geophys Res Lett 32:L24614. doi:10.1029/2005GL023915
van Haren H, Millot C (2009) Slantwise convection: a candidate for homogenization of deep newly formed dense waters. Geophys Res Lett 36:L12604. doi:10.1029/2009GL038736
van Haren H, Millot C, Taupier-Letage I (2006) Fast deep sinking in Mediterranean eddies. Geophys Res Lett 33:L04606. doi:10.1029/2005GL025367
Voorhis AD, Webb DC (1970). Large vertical currents observed in a winter sinking region of the northwestern Mediterranean. Cah océanogr 22:571-580

![Fig. 1 Site and hydrography. a) Western-Mediteranean Sea with observational site *. Depth contours every 500 m for [500, 2500] m and 2750 m. b) Typical local density anomaly profiles referenced to a pressure of 2000 dbar observed using shipborne CTD in April 2005 (blue; stopped at z = -2500 m) and February 2006 (red) during mooring deployment and recovery cruises, respectively. For reference, particular density gradient slopes are given (see text). To the left, the mooring is given schematically, with current meter (CM) depths (same colours as in Figs 2a,b, 3a,b; light-blue: only Tdata) and range of upward looking ADCP (yellow). The local seafloor is at the x-axis.](https://hackernoon.imgix.net/images/fWZa4tUiBGemnqQfBGgCPf9594N2-3xc3zxe.png?auto=format&fit=max&w=1920)









如有侵权请联系:admin#unsafe.sh